Security Model

Introduction

EigenDA is a high-throughput, decentralized data availability (DA) layer built on EigenLayer, designed to ensure that any data confirmed as available by the protocol can be reliably retrieved by clients. The system distinguishes between two core failure modes:

• Safety failure: The DA layer issues a valid availability certificate, but users are unable to retrieve the corresponding data.
• Liveness failure: Data that should be available—i.e., properly paid for and within system throughput bounds—is not served to users.

EigenDA mitigates these risks through a BFT security model backed by restaked collateral. Operators participating in the DA layer are delegated stake via EigenLayer, including ETH, EIGEN, and customized tokens.

Additionally, EIGEN slashing introduces strong accountability: in the event of a safety failure, stake can be slashed, penalizing operators who sign availability attestations for data they do not actually serve. Extra economic alignment is also provided by token toxicity.

On this page, we present a technical analysis of EigenDA's security guarantees. We use the terms validator and operator interchangiblity in this document.

Cryptographic Primitives

The encoding module is used for extending a blob of data into a set of encoded chunks which can be used to reconstruct the blob. The correctness of the encoding is proven by the proving module. The encoding and proving module needs to satisfy two main properties:

• Any collection of unique, encoded chunks of a sufficient size can be used to reconstruct the original unencoded blob.
• Each chunk can be paired with an opening proof which can be used to verify that the chunk was properly derived from a blob corresponding to a particular commitment.

To achieve these properties, the module provides the following primitives:

• EncodeAndProve. Extends a blob of data into a set of encoded chunks. Also produces opening proofs and blob commitments.
• Verify. Verifies a chunk against a blob commitment using an opening proof.
• Decode. Reconstructs the original blob given a sufficiently sized collection of encoded chunks.

EigenDA implements the encoding module using Reed Solomon encoding, together with KZG polynomial commitments and opening proofs. More details about the encoding and proving module can be found in the code spec.

Quorums and Security Models

In EigenDA, there are three different kinds of quorums where different assets (restaked-ETH, EIGEN and customized tokens of roll-ups) are delegated to the operators. Different quorums provide different security guarantees. All three kinds of quorums must simultaneously fail for a safety attack to be successfully executed, providing multi-layered security assurance.

The three security models in EigenDA, along with their corresponding quorums, are outlined below:

• BFT security: ETH, EIGEN and Custom Quorum
• Cryptoeconomic security: EIGEN Quorum
• Token Toxicity: Custom Quorum

We begin by giving an overview of each security model and how it contributes to EigenDA’s overall resilience: BFT security ensures both safety and liveness of the system as long as the share of stake or voting power held by malicious validators stays below a certain threshold. Cryptoeconomic security goes a step further—if an attacker misbehaves, they not only need to control a significant amount of stake, but they also risk losing it through slashing. This makes attacks financially unappealing. Token toxicity adds another layer of incentive alignment. When validators misbehave, the native token may drop in value, leading to losses for token holders who delegated their stake to those validators. This dynamic encourages stakeholders to carefully choose trustworthy operators.

In the rest of this page, we provide a detailed analysis of how the three kinds of security are satisfied.

BFT Security Model

The BFT security model ensures system safety and liveness as long as the stake delegated to malicious validators remains below a predefined threshold. We begin by analyzing the reconstruction guarantee of our chunk assignment algorithm, and then proceed to prove the BFT security of EigenDA.

Chunk Assignment Algorithm

In this section, we describe how the encoded chunks are allocated to each validator based on their stake, and prove the reconstruction property of the assignment.

Parameters

The allocation of data among the EigenDA validators is governed by chunk assignment logic which takes as input a set of BlobParameters which are linked to the blob Version by a mapping in the EigenDAServiceManager contract. The BlobParameters consist of:

• NumChunks - The number of encoded chunks that will be generated for each blob (must be a power of 2).
• CodingRate - The total size of the encoded chunks divided by the size of the original blob (must be a power of two). Note that for representational purposes, this is the inverse of the standard coding rate used in coding theory.
• MaxNumOperators - The maximum number of operators which can be supported by the blob Version.

The chunk assignment logic provides the following primitives:

• GetChunkAssignments. Given a blob version and the state of the validators, generates a mapping from each chunk index to a validator.
• VerifySecurityParameters. Validates whether a given set of security parameters is valid with respect to a blob version.

For the purposes of modeling, we let $m_i$ denote the number of chunks which the assignment logic maps to an operator $i$. We also denote the NumChunks defined by the blob version as $m$, the CodingRate as $r$, and the MaxNumOperators as $n$. Any set of $m/r$ unique chunks can be used to recover the blob. We let $\alpha_i = rm_i/m$, which is the number of chunks assigned to validator $i$, divided by the number of chunks needed to recover the blob. We also denote $\eta_i$ as the percentage of quorum stake which is assigned to the validator $i$. The minimum percentage of the total stake that a group of validators must collectively hold in order to possess enough chunks to recover the blob is denoted by $\gamma$. The key terminology is summarized below for reference:

Term	Symbol	Description
Max Validator Count	$n$	The maximum number of validator nodes participating in the system (currently $n =200$)
Validator Set	$N$	Set of all the validators. $\|N\|$ is the total number of validator nodes participating in the system.
Total Chunks	$m$	The total number of chunks after encoding (currently $m=8192$)
Coding Rate	$r$	The total number of chunks after encoding / total number of chunks before encoding (currently $r=8$)
Percentage of blob per validator	$\alpha_i$	$\alpha_i = rm_i/m$, the percentage of chunks required to reconstruct the blob assigned to validator $i$ in a quorum
Num of Chunks Assigned	$m_i$	The number of chunks assigned to validator $i$ in a quorum
Validator Stake	$\eta_i$	The stake proportion of validator $i$ in a quorum ($0 \le \eta_i \le 1$, and $\sum_{i} \eta_i = 1$)
Reconstruction Threshold	$\gamma$	The minimum percentage of total stake required for a group of validators to successfully reconstruct the blob

Properties for a Single Quorum

We start by describing the chunk assignment logic and the properties we aim to satisfy within a single quorum. For each quorum, the assignment algorithm is designed to satisfy the following properties:

1. Non-overlapping assignment: $\sum_i m_i \le m$.
2. Reconstruction: If a blob passes VerifySecurityParameters, then for any set of validators $H \subseteq N$ such that $\sum_{i \in H} \eta_i \ge \gamma$, we must have $\sum_{i\in H} \alpha_i \ge 1$.

Note that EigenDA supports multiple quorums, and a single validator may participate in several of them. To improve efficiency, we introduced optimizations that minimize the number of chunks assigned to each validator, while still preserving the required availability and safety properties within each quorum.

Specification

GetChunkAssignments

The number of chunks assigned to validator $i$ is calculated by:

$$m_i= \left\lceil\eta_i(m- n)\right\rceil,$$

where $n$ is the maximum number of operators. We rank the validators in a deterministic order and then assign chunks sequentially until each validator $i$ has received $m_i$ chunks.

VerifySecurityParameters

Verification succeeds as long as the following condition holds:

$$n \le m(1 - \frac{1}{r\gamma})$$

Note that from the inequality above, we can derive that $\gamma \ge \frac{m}{(m-n)r} > 1/r$, which implies that the reconstruction threshold is greater than the theoretical lower bound of stake needed for reconstruction $(1/r)$, due to the chunk assignment logic.

Proof of Properties

We want to show that for a blob which has been distributed using GetChunkAssignments and which satisfies VerifySecurityParameters , the following properties hold:

1. Proof of Non-overlapping assignment. Note that: $\sum_{i} m'_{i} \le \sum_{i} [\eta_{i} (m - n)+1] = m- n + \|N\| \le m$ Therefore, the chunks assigned to all the validators are greater than the chunks assigned to the validators, ensuring that there is no overlapping between the chunks assigned to each of them.

2. Proof of Reconstruction. We show that $\alpha_i \ge \eta_i /\gamma$:

$$m_i \ge \eta_i(m - n) \ge \eta_i(m - m(1-1/r\gamma))=\eta_i m/(r\gamma)$$ $$\Rightarrow \alpha_i = rm_i/m \ge \eta_i/\gamma$$

Therefore, $\sum_{i\in H} \alpha_i \ge \sum_{i\in H} \eta_i/\gamma \ge 1$ when $\sum_{i \in H} \eta_i \ge \gamma$. This means that any set of validators holding at least a $\gamma$ fraction of the total stake collectively owns at least as many chunks as are required to reconstruct one blob, i.e., at least $m / r$ chunks. Since there is no overlap between the chunks assigned to each validator within a quorum, the union of their assigned chunks forms a set that can be used to reconstruct the full blob.

Optimization: Minimizing Chunks Assigned to Each Validator

In EigenDA, a client may require validators from multiple quorums to store data and sign a DA certificate for a blob. A validator may participate in more than one quorum at the same time. A naive approach to assigning chunks is to run the chunk assignment algorithm described above independently for each quorum and send each validator the chunks they are supposed to store in each quorum separately. However, this method results in validators storing the sum of workloads from all quorums they participate in, which is inefficient and degrades performance.

To reduce the number of chunks assigned to each validator, we apply the following strategies:

1. An optimization algorithm is designed to increase the overlap of chunks assigned to each validator across multiple quorums. Furthermore, each validator is sent only the union of their assigned chunks across all quorums, reducing redundancy and minimizing overall storage overhead.

2. The number of unique chunks assigned to any validator is capped at $m / r$.

We analyse the impact of the optimization as follows:

1. The optimization algorithm does not change the number of chunks assigned to each validator within any quorum. The non-overlapping property is also preserved. Therefore, the reconstruction guarantees of each quorum remain unchanged.

2. We now show that the reconstruction property still holds after applying the capping:

• Case 1: If no validator in the choosen set of validators who have at least $\gamma$ stake is assigned more than $m / r$ unique chunks, the cap has no effect. The reconstruction property remains intact.

• Case 2: If a validator in the chosen set is assigned more than $m / r$ chunks, the cap reduces their allocation to exactly $m / r$ chunks. Since this validator alone holds $m / r$ unique chunks, they can reconstruct the blob. Therefore, the validator set as a whole also retains the ability to reconstruct the blob.

Safety and Liveness Analysis

In this section, we define and prove the safety and liveness properties of EigenDA, building on the reconstruction property established above.

The Byzantine liveness and safety properties of a blob are specified by a collection of SecurityThresholds.

• ConfirmationThreshold (also denoted as $\eta_C$) - The confirmation threshold defines the minimum percentage of stake which needs to sign to make the DA certificate valid.
• SafetyThreshold (also denoted as $\eta_S$) - The safety threshold refers to the minimum percentage of total stake an attacker must control to make a blob with a valid DA certificate unavailable.
• LivenessThreshold(also denoted as $\eta_L$) - The liveness threshold refers to the minimum percentage of total stake an attacker must control to cause a liveness failure.

We start with the assumptions to guarantee safety and liveness:

1. To guarantee safety, we assume that the adversary controls less than the SafetyThreshold percentage of the total stake.
2. To guarantee liveness, we currently rely on a trusted disperser that does not censor clients’ blob disperser requests. We will soon introduce decentralized dispersal to remove this trust assumption. Additionally, to ensure liveness, we assume the adversary is delegated with less than LivenessThreshold percentage of the total stake.

In the following part, we prove that the security and liveness holds when the assumptions are satisfied.

First, we prove the security of our protocol: If the malicious party is delegated with less than $\eta_S = \eta_C - \gamma$ percentage of stake in the quorum, when a DA certificate is issued, any end-user can retrieve the blob within the time window during which the blob is supposed to be available. Proof: Since at least $\eta_C = \eta_S + \gamma$ percentage of the stake signed for the blob in order for the DA certificate to be issued and the maximum adversarial stake percentage is $\eta_S$, there is a set of honest validators $H$ who are delegated with at least $\eta_C - \eta_S = \gamma$ percentage of the stake and signed the blob. As we proved in the previous section, for any set of validators $H$ such that $\sum_{i \in H} \eta_i \ge \gamma$, we must have $\sum_{i\in H} \alpha_i \ge 1$, which means $H$ holds a set of chunks whose size is large enough to recover the blob and will be able to recover and serve the blob to the end-user.

Second, we prove the liveness of our protocol: If the malicious party controls less than $\eta_L = 1 - \eta_C$ portion of stake in the quorum, when a client calls the dispersal function, they will eventually get back a DA certificate for the blob they submitted, assuming that the disperser is honest. This simply follows from the fact that an honest disperser would encode and distribute the chunks following the protocol and all the honest validators would send their signatures to the dispersal when they receive and verify the chunks they are assigned. Therefore, since the portion of honest stake is greater than $\eta_C$, enough signatures will be collected by the disperser and a DA certificate will be issued in the end.

Encoding Rate and Security Thresholds

In the previous section, we demonstrated that the system is secure—that is, both the safety and liveness properties are upheld—provided the adversarial stake remains below a certain threshold. In this section, we aim to determine the minimum required encoding rate based on a given adversarial stake percentage, in order to quantify the system’s overhead.

Suppose the maximum adversarial stake that can be used to compromise safety is denoted by $\eta_s$, and the maximum stake that can be used to compromise liveness is  $\eta_l$. To ensure the security of the system, the following conditions must be satisfied: $\eta_s \le \eta_S = \eta_C - \gamma$ and $\eta_l \leq \eta_L = 1 - \eta_C$. From these inequalities, we can derive: $\gamma \le 1 - \eta_s - \eta_l$. Also, recall that $\gamma \ge \frac{m}{(m-n)r}$ . This leads to the following constraint on the encoding rate $r$:

$$\frac{m}{(m-n)r} \leq 1 - \eta_s - \eta_l \Leftrightarrow r \ge \frac{m}{(m-n)(1-\eta_s-\eta_l)}$$

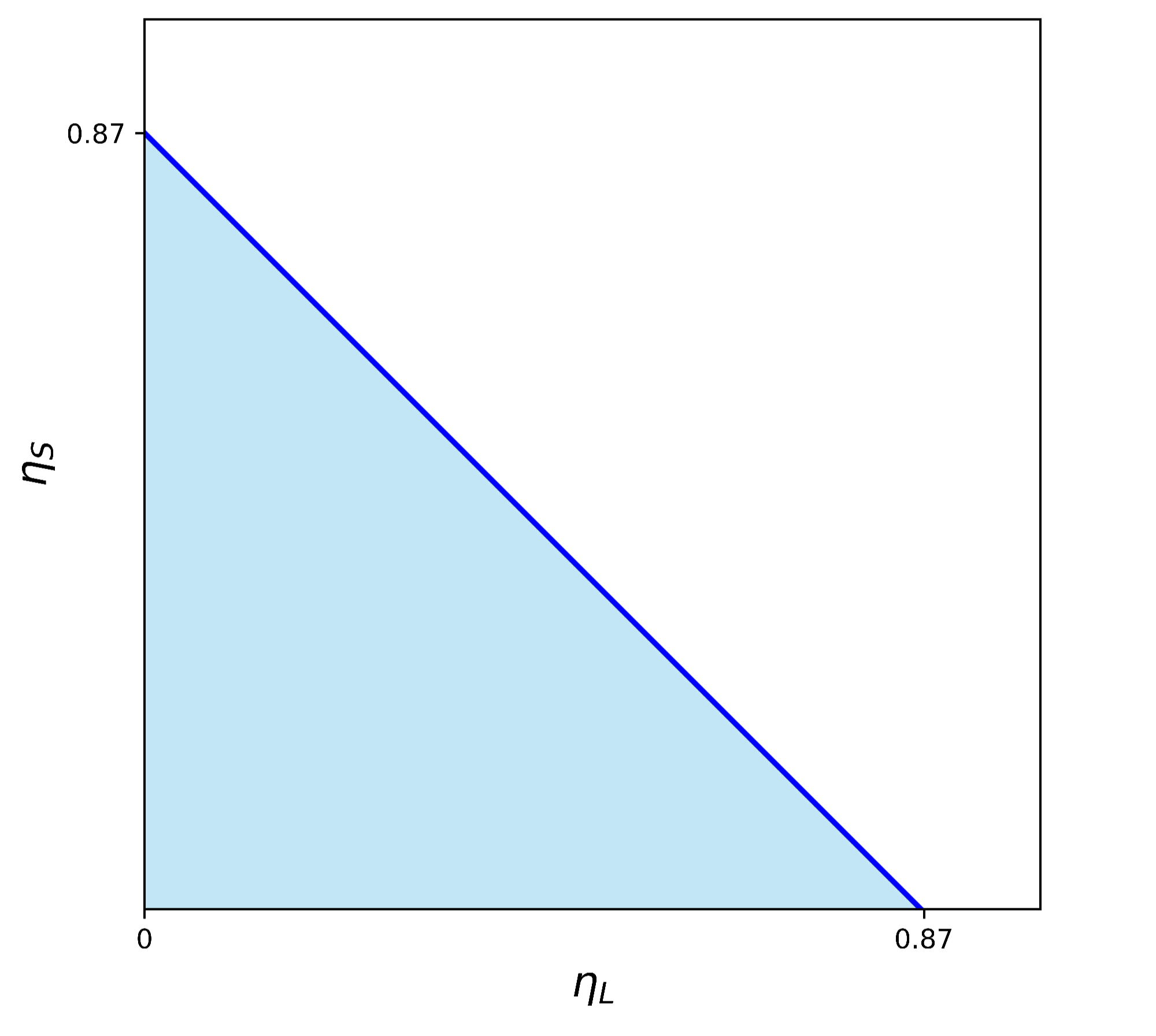
Assuming the system aims to tolerate up to 54% adversarial stake for safety attacks ($\eta_s = 54 \%$) and and up to 33% adversarial stake for liveness attacks ($\eta_l = 33 \%$), and given system parameters $m = 8192$ and $n = 200$, we compute: $r \ge 8192 / (8192-200)/(1-54\% -33\%)= 7.9$ . Therefore, to ensure system security under these adversarial conditions, the encoding rate must be at least 7.9.

In our implementation, we choose an encoding rate of $r = 8$ (which means that our system operates with a 8X overhead). Therefore, we can compute the minimum value of $\gamma$ as $\gamma_{min} = \frac{8192}{(8192-200)*8} = 0.13$. This yields the following safety and liveness threshold: $\eta_S = \eta_C - 0.13$ and $\eta_L = 1 - \eta_C$. Combining the two gives: $\eta_S + \eta_L = 0.87$. The safety-liveness threshold trade-off of our system, given the chosen parameters, is illustrated in the figure below. Any adversary with a stake profile $(\eta_s, \eta_l)$ that lies below the line in the plot falls within the defensible region of the system. 

Cryptoeconomic Security Model

In addition to BFT security, the EIGEN quorum provides cryptoeconomic security as an extra layer of protection. Cryptoeconomic security guarantees that if the safety of the system is compromised, a certain portion of stake will be slashed. This creates a strong disincentive for attacking the system. A protocol is considered cryptoeconomically secure when the total cost of an attack always exceeds the total profit from an attack. However, like many other attacks, the profit possible from a DA withholding attack can be difficult to quantify. That’s why the emphasis is placed on slashing: the ability to penalize misbehaving validators is key to maintaining system safety.

Intersubjective Slashing with Token Forking

If BFT security fails and data certified by a valid DA certificate becomes unretrievable, any community member can raise a data unavailability alarm. Once triggered, other community members will attempt to retrieve and verify the data. If a sufficient number of community members confirm that safety has indeed been compromised, they can initiate a token fork to slash the stake of dishonest validators (see more in the EIGEN Token Whitepaper).

DAS: Fraud Detection Tool for Slashing

As discussed in Security FAQs , the Data Availability Sampling (DAS) protocol is useful for fraud detection, especially for light nodes with limited resources, though it has limitations. We are actively developing the DAS protocol for EigenDA to address these limitations, providing better support for fraud detection and intersubjective slashing. A detailed white paper will be released soon.

Token Toxicity Security Model

In addition to BFT security, the custom quorum provides an extra security guarantee through Token Toxicity. Token toxicity refers to the phenomenon where the value of a rollup's native token declines sharply when the rollup fails to function properly. Specifically, if DA isn't ensured for a rollup, market confidence in the roll-up service declines, causing its token price to drop. This economic incentive encourages holders of the roll-up's custom token to delegate their stakes only to trusted operators, minimizing the risk of data unavailability and potential loss in token value.

In conclusion, EigenDA’s security model combines BFT security, cryptoeconomic security, and token toxicity to create a robust, multi-layered defense against safety and liveness failures.